A bitwise solution to the N Queens problem in Javascript

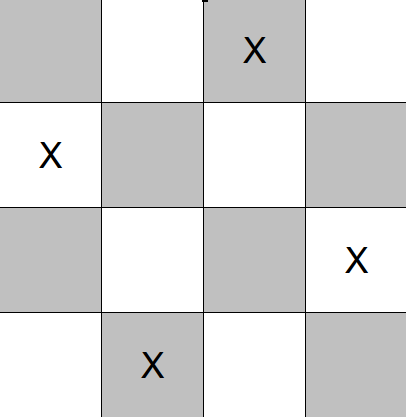
The N Queens problem is a fairly well-known puzzle in the computer science community. The goal is to place N queens on an N x N chessboard in such a way that none of the queens can attack one another.

Above is an example solution for N=4 (that is, placing 4 queens on a 4x4 chessboard such that none of them can attack another).

As you might imagine, this problem gets harder as N increases (this is a HUGE understatement), especially if your goal is to count all possible solutions, rather than to find just one solution. In fact, as of this writing, no one in the world has counted all the solutions for N > 27 (the world record is N = 27).

This blog post will go through my Javascript implementation of the algorithm described in this paper by Martin Richards. The algorithm is very efficient because it takes advantage of bitwise operators.

If you have never seen the N Queens problem before, I'd recommend trying it out yourself before checking out this code. It's fun to try on your own, and you'll get more out of this walkthrough if you've at least attempted to implement your own algorithm beforehand. (This bitwise implementation was my fourth implementation, and is MUCH faster than my first attempt).

That being said, let's get started:

The goal: Write a function that will find all possible solutions to the N queens problem for a given N.

The algorithm described in the paper (which I'll be implementing in this post), basically approaches the problem like this:

• Queens can attack diagonally, vertically, or horizontally. As a result, there can only be one queen in each row, one in each column, and at most one on each diagonal.
• Since we know there can only one queen per row, we will start at the first row, place a queen, then move to the second row, place a second queen, and so on until either a) we reach a valid solution or b) we reach a dead end (ie. we can't place a queen such that it is "safe" from the other queens).
• Since we are only placing one queen per row, we don't need to worry about horizontal attacks, since no queen will ever be on the same row as another queen.
• That means we only need to check three things before placing a queen on a certain square: 1) The square's column doesn't have any other queens on it, 2) the square's left diagonal doesn't have any other queens on it, and 3) the square's right diagonal doesn't have any other queens on it.
• If we ever reach a point where there is nowhere safe to place a queen, we can give up on our current attempt and immediately test out the next possibility.

Before we start, you may want to take a brief look at Javascript's bitwise operators. No need to go too in-depth yet--I'll show you the relevant ones for this implementation later on.

DO, however, make sure you're familiar/comfortable with the fact that computers store data (such as integers) as sequences of bits.

eg. The number 5 is represented in binary as 0101.

Ok, enough preparation! Here's the full solution (I'll walk through it below):

countNQueensSolutions = function(n) {
  //Keeps track of the # of valid solutions
  var count = 0;

  //Helps identify valid solutions
  var done = Math.pow(2,n) - 1;

  //Checks all possible board configurations
  var innerRecurse = function(ld, col, rd) {

    //All columns are occupied,
    //so the solution must be complete
    if (col === done) {
      count++;
      return;
    }

    //Gets a bit sequence with "1"s
    //whereever there is an open "slot"
    var poss = ~(ld | rd | col);

    //Loops as long as there is a valid
    //place to put another queen.
    while ( poss & done ) {
      var bit = poss & -poss;
      poss -= bit;
      innerRecurse((ld|bit)>>1, col|bit, (rd|bit)<<1);
    }
  };

  innerRecurse(0,0,0);

  return count;
};

First let's talk about the innerRecurse function. You'll notice that it accepts 3 parameters: ld, col, and rd. Each of these is technically an integer, but the algorithm takes advantage of the fact that an integer is represented by a sequence of bits. So, think of each of these parameters as a sequence of N bits.

Each bit in each of the parameters represents whether the corresponding location on the current row is "available".

For example:

• For N=4, col having a value of 0010 would mean that the 3rd column is already occupied by a queen.

• For N=8, ld having a value of 00011000 at row 5 would mean that the top-left-to-bottom-right diagonals that pass through columns 4 and 5 of that row are already occupied by queens.

Below is a visual aid for ld, rd, and cols that I shamelessly copied from the paper

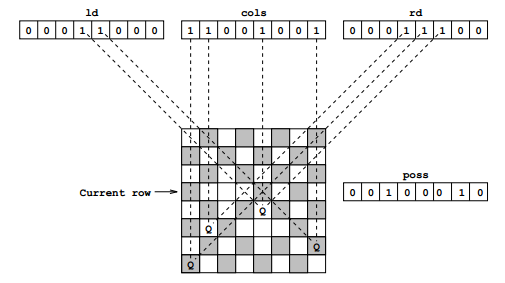
In my implementation, ld is meant to represent the diagonal from the top left to the bottom right, rd represents the diagonal from the top right to the bottom left, and col represents the columns. If you're following along with the paper, you may notice that this isn't exactly the same way the author thinks about things, but it ends up being roughly the same implementation either way.

innerRecurse()

So, let's say we've just called the innerRecurse function and passed in 3 all-zero bit sequences. This is what I'm doing on the line that says innerRecurse(0,0,0);.

If N=4, we can think of col, ld, and rd as all being equal to 0000. Since we just started the process (and haven't placed any queens yet), this makes sense (none of the columns or diagonals are "taken" yet).

The first if statement

The first if statement in the innerRecurse function just checks whether a valid solution has been found yet. It does this by checking whether all the columns (represented by col) have been occupied by queens. Since the algorithm never places a queen illegally (ie. when it can attack or be attacked), we know that if all the columns have been filled, we must have a valid solution.

Obviously, if this is our first pass through the innerRecurse function, none of the columns are occupied, and so the code initially skips the first if block.

var poss

Next, the code initializes the variable poss. All that's happening here is we're taking col, ld, and rd, and if any of the columns are "under attack", we mark that column as 0 in poss, basically meaning "we can't put a queen in this column".

For example, let's say that after some number of iterations we have:

• ld = 0001
• rd = 0101
• col = 1001

The code (ld | rd | col) just does an "OR" operation, ending up with the bit sequence 1101. Then, adding the ~ in front of that expression causes the resulting bit sequence to "flip" (so all zeroes become ones and vice versa), and poss would be set to ~(1101), which is just 0010.

So, again, the poss variable just represents the columns in the current row that are not "under attack" from any other queens.

The first two lines of while loop

All that's happening in the while loop is the following:

• The first line, var bit = poss & -poss; just stores the first non-zero bit (ie. the first available location) in a variable called 'bit'.

• That 'bit' (which, again, represents a column on the chessboard, so if bit was 0010, it would mean the 3rd column of the current row), is where we will be placing our next queen. So the line poss -= bit just marks that position in the current row as being "taken" by flipping that column in poss to zero. This way, when the while loop continues, we'll know not to try that location again.

The last statement in the while loop

innerRecurse((ld|bit)>>1, col|bit, (rd|bit)<<1); is, in my opinion, the most confusing line in this entire function. Let's break it down.

The operators >> 1 and 1 << simply move all the bits in a bit sequence one digit to the right or left, respectively. So calling (rd|bit)<<1 simply says: combine rd and bit with an OR operation, then move everything in the result to the left by one digit.

• More specifically, if rd is 0001 (meaning that the top-right-to-bottom-left diagonal through column 4 of the current row is occupied), and bit is 0100 (meaning that we are planning to place a queen in column 2 of the current row), (rd|bit) results in 0101 (meaning that after we place a queen in column 2 of the current row, the second and the fourth top-right-to-bottom-left diagonals will be occupied).

• Now, if add in the << operator, we get (rd|bit)<<1, which takes the 0101 we worked out in our previous bullet point, and moves everything to the left by one. The result, therefore, is 1010.

Now here's the really confusing part: why do we move everything over by one digit before calling innerRecurse again?

If we start at the top row and move down, every time we go down to a new row, we need to keep our "occupied diagonal" tracking variables, ld and rd, up to date.

So, to use the image below as an example, if we place a queen in the 3rd column of the top row, then col, ld, and rd at that moment will be 0010, 0010, and 0010, respectively.

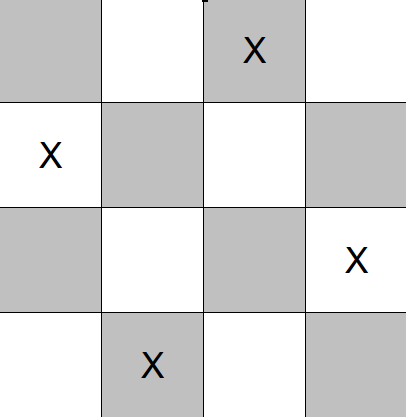
However, when we move on to the next row by calling innerRecurse again, we can see that in row two, the second, third, AND fourth columns are all "under attack" by the one queen we've placed so far. More specifically, the third column is occupied (so col is 0010), the top-left-to-bottom-right diagonal through column 4 of the second row is occupied (so ld should be 0001), and the top-right-to-bottom-left diagonal through column 2 of the second row is occupied (so rd should be 0100).

That is why we need to shift the diagonals each time we "go down a row": otherwise, our knowledge of which diagonals are "occupied" is not correct for the current row.

As you can see from the above example, calculating var poss = ~(ld | rd | col) will yield 1000, indicating that the ONLY safe location for row 2 is the first column.

the done variable

Just to wrap everything up, the "done" variable simply allows me to not worry about any bits beyond the Nth. Most computers are either 32 bits or 64 bits, so in reality, all integers are stored with that many bits. done simply has a bit sequence with 1 for every entry up to the Nth. For example, when N=5, done will equal 11111.

By writing things like poss & done, I automatically set all other bits to zero, meaning that I don't have to worry about them.

...and that's pretty much it! The code loops through, recursively trying out different valid positions and quickly eliminating invalid solutions.

Because invalid solutions are ignored so quickly (because the while loop will end), and because we use bitwise operators for nearly all calculations, the result is a very fast, very efficient algorithm for counting the number of solutions to the N queens problem!

Here are some solutions:

N     |  # of Solutions
------|-----------------
4     |   2
5     |   10
6     |   4
7     |   40
8     |   92
9     |   352
10    |   724
11    |   2680
12    |   14200
13    |   73712
14    |   365596
15    |   2279184

Tag

• javascript
• algorithms