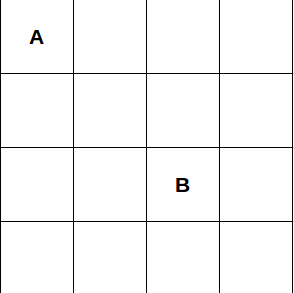
Picture this. You're on a two-dimensional grid, on a square labeled "A", and you need to find the shortest path to a square labeled "B".
Also, you're given the map pictured above.
Not very difficult, huh? As a human, you can easily figure out several optimal paths from square "A" to square "B" (and in the space of about half a second).
Now let's say things are a little bit more complicated. What if the map looked like this?

This is (slightly) more difficult. You could probably still solve this in a very short amount of time, but you can see that if we had a very large board with a large number of obstacles, this problem would start to take more effort to solve.
Well, it turns out that with a fairly simple algorithm, a computer can solve this and even mind-bogglingly more difficult pathfinding problems. Let's learn how to write this algorithm!
A basic path-finding algorithm (coded in Javascript)
The technique we'll be using is called "Breadth-First Search".
Feel free to google it on your own, but basically it just means we're going to check every possible path of length 1, then every possible path of length 2, and so on until we find the first shortest possible path that will take us from square "A" to square "B".
This isn't quite as inefficient as it sounds (and it will take a very large pathfinding problem before this approach becomes infeasible for a basic modern computer), but do keep in mind that the memory and time required to solve a pathfinding problem with this method increase relatively quickly as the size of the board increases.
Fun Fact: My team and I provide a version of this algorithm for our daily Artificial Intelligence game, Javascript Battle. If you want to check it out, follow the directions on the site to sign up, then look at the helpers.js file in your forked repository.
Step 1: We need a queue
First, we need a queue data structure to keep track of all the squares we're planning to check to determine the best path. Think of this as a "to-do" list that prioritizes how we approach our search.
// We'll use an array* to simulate a "queue" data structure
var q = [];
// * More advanced readers: Note that it would technically be faster to implement this queue as a linked list, but this is simpler
Step 2: We need to add new locations to the queue as we "discover" them
Remember, the queue is sort of our "to-do" list of places to explore. We want to explore the closest places to our start location first (this means that we want to make sure that closer locations get added to our queue before locations that are farther away).
So, what's the place on the board that is closest to our start location? Trick question: the closest place IS our start location. So to start we'll put our start location in our queue.
Step 3: Now we search!
At this point, we will do the following sequence:
- Pull the first location off of the queue
- Loop through the locations that are 1 "move" away from the location you just pulled off the queue (in this example, the tiles to the North, South, East, and West of the current tile)
- If one of these locations is the goal--you're done!
- Otherwise: if and only if the location has not yet been visited and is valid (ie. is on the board and is not an "obstacle"), add that new location to the end of the queue.
- Repeat the process...(pull the first location off of the queue, etc.)
We will keep doing this until we find a goal state (the third bullet point) or until we run out of locations to search (the queue becomes empty).
In the first case, we will have found the shortest path to a solution (we know it's the shortest path because we are always adding the closest locations first).
In the second case, we will have determined that there IS no valid path to the end location (because when the queue empties, it means there are no more valid locations to explore).
It may already be clear to you that following the above steps will yield this result. In case it's not yet clear (which is totally normal, given that you only just read those bullet points), let's do an example...
A quick example: Let's walk through our algorithm step-by-step
To re-use our example above: let's say we are at location "A" and we want to go to location "B". Let's try to solve this (fairly simple) problem using our algorithm.

Step 1: We need a queue, which I'll represent in javascript array notation
Queue = []
Step 2: We need to add our start location to the queue.
I'll represent each location as a coordinate like so:
(distance from top, distance from left)
Queue = [(0,0)]
Step 3: Follow the sub-steps...
- Get the first location off the queue:
- Location:
(0,0), Queue =[]
- Location:
- Loop through the locations around this location:
- North: Invalid (off the top of the grid)
- East: New location:
(0,1), Queue:[ (0,1) ] - South: New location:
(1,0), Queue:[ (0,1), (1,0) ] - West: Invalid (off the left of the grid)
- Repeat the process (I'll just list out the state of the queue each time it changes)
- Get the next location off the queue...Location:
(0,1), Queue =[ (1,0) ] - Add neighboring valid location(s) to the queue...Queue =
[ (1,0), (0,2) ] - Get the next location off the queue...Location:
(1,0), Queue =[ (0,2) ] - Add neighboring valid location(s) to the queue...Queue =
[ (0,2), (2,0) ] - Get the next location off the queue...Location:
(0,2), Queue =[ (2,0) ] - Add neighboring valid location(s) to the queue...Queue =
[ (2,0), (0,3) ] - Get the next location off the queue...Location:
(2,0), Queue =[ (0,3) ] - Add neighboring valid location(s) to the queue...Queue =
[ (0,3), (3,0) ] - Get the next location off the queue...Location:
(0,3), Queue =[ (3,0) ] - Add neighboring valid location(s) to the queue...Queue =
[ (3,0) ](in the top right corner, there are no valid, unvisited locations nearby, so nothing is added to the queue) - Get the next location off the queue...Location:
(3,0), Queue =[ ] - Add neighboring valid location(s) to the queue...Queue =
[ (3,1) ] - Get the next location off the queue...Location:
(3,0), Queue =[ ] - Add neighboring valid location(s) to the queue...Queue =
[ (3,1) ] - Get the next location off the queue...Location:
(3,1), Queue =[ ] - Add neighboring valid location(s) to the queue...Queue =
[ (3,2) ] - Get the next location off the queue...Location:
(3,2), Queue =[ ] - Finally! When we go to add neighboring valid locations that are within one square of (3,2), we realize that (2,2) is our goal, and the algorithm stops! We have successfully found the shortest path between location A and location B!
- Get the next location off the queue...Location:
Let's Code It:
Let's actually set up what the "grid" would look like in code:
// Create a 4x4 grid
// Represent the grid as a 2-dimensional array
var gridSize = 4;
var grid = [];
for (var i=0; i<gridSize; i++) {
grid[i] = [];
for (var j=0; j<gridSize; j++) {
grid[i][j] = 'Empty';
}
}
// Think of the first index as "distance from the top row"
// Think of the second index as "distance from the left-most column"
// This is how we would represent the grid with obstacles above
grid[0][0] = "Start";
grid[2][2] = "Goal";
grid[1][1] = "Obstacle";
grid[1][2] = "Obstacle";
grid[1][3] = "Obstacle";
grid[2][1] = "Obstacle";
Now that we have a representation of our "grid": Let's write a function that takes a start location and a board array, and returns an array listing the shortest path (and then we'll pull it all together).
Please note: it takes a bit more complexity (as you'll see) to actually return the shortest path. However, you'll notice that at the core, we are simply implementing the algorithm described above.
// Start location will be in the following format:
// [distanceFromTop, distanceFromLeft]
var findShortestPath = function(startCoordinates, grid) {
var distanceFromTop = startCoordinates[0];
var distanceFromLeft = startCoordinates[1];
// Each "location" will store its coordinates
// and the shortest path required to arrive there
var location = {
distanceFromTop: distanceFromTop,
distanceFromLeft: distanceFromLeft,
path: [],
status: 'Start'
};
// Initialize the queue with the start location already inside
var queue = [location];
// Loop through the grid searching for the goal
while (queue.length > 0) {
// Take the first location off the queue
var currentLocation = queue.shift();
// Explore North
var newLocation = exploreInDirection(currentLocation, 'North', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
} else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// Explore East
var newLocation = exploreInDirection(currentLocation, 'East', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
} else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// Explore South
var newLocation = exploreInDirection(currentLocation, 'South', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
} else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
// Explore West
var newLocation = exploreInDirection(currentLocation, 'West', grid);
if (newLocation.status === 'Goal') {
return newLocation.path;
} else if (newLocation.status === 'Valid') {
queue.push(newLocation);
}
}
// No valid path found
return false;
};
// This function will check a location's status
// (a location is "valid" if it is on the grid, is not an "obstacle",
// and has not yet been visited by our algorithm)
// Returns "Valid", "Invalid", "Blocked", or "Goal"
var locationStatus = function(location, grid) {
var gridSize = grid.length;
var dft = location.distanceFromTop;
var dfl = location.distanceFromLeft;
if (location.distanceFromLeft < 0 ||
location.distanceFromLeft >= gridSize ||
location.distanceFromTop < 0 ||
location.distanceFromTop >= gridSize) {
// location is not on the grid--return false
return 'Invalid';
} else if (grid[dft][dfl] === 'Goal') {
return 'Goal';
} else if (grid[dft][dfl] !== 'Empty') {
// location is either an obstacle or has been visited
return 'Blocked';
} else {
return 'Valid';
}
};
// Explores the grid from the given location in the given
// direction
var exploreInDirection = function(currentLocation, direction, grid) {
var newPath = currentLocation.path.slice();
newPath.push(direction);
var dft = currentLocation.distanceFromTop;
var dfl = currentLocation.distanceFromLeft;
if (direction === 'North') {
dft -= 1;
} else if (direction === 'East') {
dfl += 1;
} else if (direction === 'South') {
dft += 1;
} else if (direction === 'West') {
dfl -= 1;
}
var newLocation = {
distanceFromTop: dft,
distanceFromLeft: dfl,
path: newPath,
status: 'Unknown'
};
newLocation.status = locationStatus(newLocation, grid);
// If this new location is valid, mark it as 'Visited'
if (newLocation.status === 'Valid') {
grid[newLocation.distanceFromTop][newLocation.distanceFromLeft] = 'Visited';
}
return newLocation;
};
// OK. We have the functions we need--let's run them to get our shortest path!
// Create a 4x4 grid
// Represent the grid as a 2-dimensional array
var gridSize = 4;
var grid = [];
for (var i=0; i<gridSize; i++) {
grid[i] = [];
for (var j=0; j<gridSize; j++) {
grid[i][j] = 'Empty';
}
}
// Think of the first index as "distance from the top row"
// Think of the second index as "distance from the left-most column"
// This is how we would represent the grid with obstacles above
grid[0][0] = "Start";
grid[2][2] = "Goal";
grid[1][1] = "Obstacle";
grid[1][2] = "Obstacle";
grid[1][3] = "Obstacle";
grid[2][1] = "Obstacle";
console.log(findShortestPath([0,0], grid));
If this is a bit hard to follow--copy the code, paste it into your browser console or run it using Node.js, and you'll see that it correctly tells you that the shortest path is:
'South', 'South', 'South', 'East', 'East', 'North'
More importantly, you can see that it can quickly calculate the shortest path to the goal in even extremely complicated pathfinding problems.